| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Example 1 (Before Exercise 2.1) | Exercise 2.1 | Example 2 to 5 (Before Exercise 2.2) |
| Exercise 2.2 | Example 6 to 9 (Before Exercise 2.3) | Exercise 2.3 |
| Exercise 2.4 (Optional) | ||
Chapter 2 Polynomials
This solutions guide focuses on Chapter 2: Polynomials, a fundamental topic in algebra that builds significantly upon concepts introduced in Class 9. Polynomials are algebraic expressions involving variables raised to non-negative integer powers, combined using addition, subtraction, and multiplication. This chapter delves deeper into their structure, properties, and particularly the crucial relationship between their zeros (the values of the variable for which the polynomial evaluates to zero) and their coefficients (the numerical constants multiplying the variable terms). Furthermore, it explores the essential technique of polynomial division through the division algorithm.
Initially, the solutions reinforce foundational concepts: identifying expressions that qualify as polynomials, determining their degree (the highest power of the variable present), and classifying them based on their degree, such as linear (degree 1), quadratic (degree 2), and cubic (degree 3) polynomials. A key graphical insight emphasized is the geometrical meaning of the zeros. For a polynomial $p(x)$, its zeros correspond precisely to the x-coordinates of the points where the graph of the equation $y = p(x)$ intersects or touches the x-axis. Understanding this connection allows for the interpretation of graphs to determine the number of real zeros a polynomial possesses – a visual link between algebra and geometry.
The algebraic core of the chapter revolves around the profound relationship between the zeros of a polynomial and its coefficients. This relationship is explored most thoroughly for quadratic polynomials, typically written in the standard form $ax^2 + bx + c$, where $a \neq 0$. If the zeros of this quadratic polynomial are denoted by $\alpha$ and $\beta$, then two fundamental relationships always hold:
- The Sum of zeros: $\alpha + \beta = -\frac{b}{a}$ (the negative of the coefficient of the x-term divided by the coefficient of the $x^2$-term).
- The Product of zeros: $\alpha\beta = \frac{c}{a}$ (the constant term divided by the coefficient of the $x^2$-term).
The solutions meticulously guide students in verifying these relationships by first finding the zeros of given quadratic polynomials (often through methods like factoring or the quadratic formula) and then calculating their sum and product to compare with $-\frac{b}{a}$ and $\frac{c}{a}$. Conversely, these relationships are used to construct a quadratic polynomial when the sum and product of its zeros are provided.
While less emphasized in typical examinations, analogous relationships exist for cubic polynomials of the form $ax^3 + bx^2 + cx + d$. If the zeros are $\alpha, \beta,$ and $\gamma$, the relationships are: $\alpha+\beta+\gamma = -\frac{b}{a}$, $\alpha\beta+\beta\gamma+\gamma\alpha = \frac{c}{a}$, and $\alpha\beta\gamma = -\frac{d}{a}$.
A critically important procedural aspect covered is the Division Algorithm for Polynomials. Similar to integer division, this algorithm states that for any two polynomials $p(x)$ (the dividend) and $g(x)$ (the divisor, where $g(x) \neq 0$), there exist unique polynomials $q(x)$ (the quotient) and $r(x)$ (the remainder) such that $p(x) = g(x) \times q(x) + r(x)$, where either the remainder $r(x)$ is the zero polynomial, or the $degree(r(x))$ is strictly less than the $degree(g(x))$. The solutions provide detailed, step-by-step illustrations of the long division process for polynomials. A key application of this algorithm arises when some zeros of a polynomial are known. If $\alpha$ is a zero of $p(x)$, then $(x-\alpha)$ is a factor. By dividing $p(x)$ by the factor(s) corresponding to the known zeros, we can find a quotient polynomial $q(x)$ of lower degree whose zeros are the remaining zeros of $p(x)$. This technique is essential for finding all zeros of higher-degree polynomials when provided with partial information. Mastering these concepts is fundamental for further study in algebra and calculus.
Example 1 (Before Exercise 2.1)
Example 1. Look at the graphs in figure below. Each is the graph of y = p(x), where p(x) is a polynomial. For each of the graphs, find the number of zeroes of p(x).
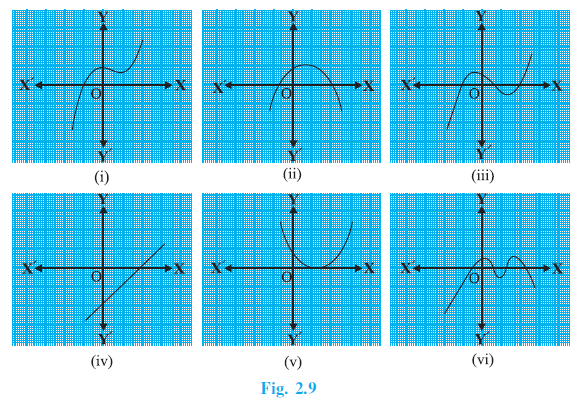
Answer:
The zeroes of a polynomial $p(x)$ are the values of $x$ for which $p(x) = 0$. Graphically, the zeroes of $p(x)$ are the x-coordinates of the points where the graph of $y=p(x)$ intersects the x-axis.
To find the number of zeroes for each graph, we count the number of points where the graph intersects or touches the x-axis.
For the given graphs:
Graph (i): The graph is a straight line parallel to the x-axis. It does not intersect the x-axis.
Number of zeroes = 0.
Graph (ii): The graph is a parabola that intersects the x-axis at two distinct points.
Number of zeroes = 2.
Graph (iii): The graph is a curve that intersects the x-axis at three distinct points.
Number of zeroes = 3.
Graph (iv): The graph is a parabola that intersects the x-axis at one point (it touches the x-axis at one point).
Number of zeroes = 1.
Graph (v): The graph is a curve that intersects the x-axis at one point.
Number of zeroes = 1.
Graph (vi): The graph is a curve that intersects the x-axis at four distinct points.
Number of zeroes = 4.
Final Answer:
The number of zeroes for each graph is as follows:
(i) 0
(ii) 2
(iii) 3
(iv) 1
(v) 1
(vi) 4
Exercise 2.1
Question 1. The graphs of y = p(x) are given in figure below, for some polynomials p(x). Find the number of zeroes of p(x), in each case.
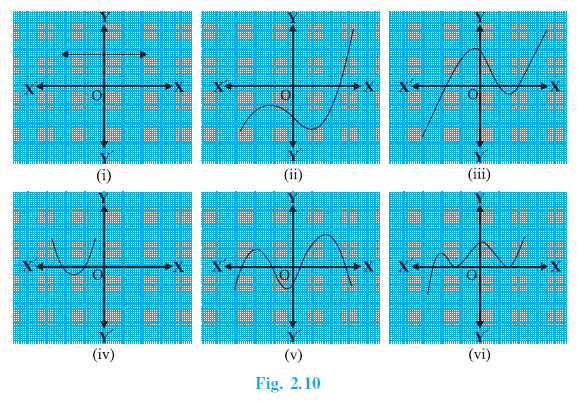
Answer:
The zeroes of a polynomial $p(x)$ are the values of $x$ for which $p(x) = 0$. Graphically, the zeroes of $p(x)$ are the x-coordinates of the points where the graph of $y=p(x)$ intersects the x-axis.
To find the number of zeroes for each graph, we count the number of points where the graph intersects or touches the x-axis.
For the given graphs:
Graph (i): The graph is a straight line that intersects the x-axis at one distinct point.
Number of zeroes = 1.
Graph (ii): The graph is a parabola that intersects the x-axis at two distinct points.
Number of zeroes = 2.
Graph (iii): The graph is a curve that intersects the x-axis at three distinct points.
Number of zeroes = 3.
Graph (iv): The graph is a parabola that intersects the x-axis at one point (it touches the x-axis).
Number of zeroes = 1.
Graph (v): The graph is a curve that intersects the x-axis at one point.
Number of zeroes = 1.
Graph (vi): The graph is a curve that intersects the x-axis at four distinct points.
Number of zeroes = 4.
Final Answer:
The number of zeroes for each graph is as follows:
(i) 1
(ii) 2
(iii) 3
(iv) 1
(v) 1
(vi) 4
Example 2 to 5 (Before Exercise 2.2)
Example 2. Find the zeroes of the quadratic polynomial x2 + 7x + 10, and verify the relationship between the zeroes and the coefficients.
Answer:
The given quadratic polynomial is $p(x) = x^2 + 7x + 10$.
The standard form of a quadratic polynomial is $ax^2 + bx + c$.
Comparing the given polynomial with the standard form, we have the coefficients: $a = 1$, $b = 7$, and $c = 10$.
To Find: The zeroes of the polynomial and verify the relationship between zeroes and coefficients.
Solution:
To find the zeroes of the polynomial $p(x)$, we set $p(x) = 0$.
$$x^2 + 7x + 10 = 0$$
We can find the zeroes by factoring the quadratic expression. We look for two numbers whose product is $10$ and whose sum is $7$. These numbers are $2$ and $5$.
Rewrite the middle term $7x$ as $2x + 5x$:
$$x^2 + 2x + 5x + 10 = 0$$
Group the terms and factor:
$$(x^2 + 2x) + (5x + 10) = 0$$
$$x(x + 2) + 5(x + 2) = 0$$
Factor out the common binomial factor $(x+2)$:
$$(x + 2)(x + 5) = 0$$
For the product of two factors to be zero, at least one of the factors must be zero.
Case 1: $x + 2 = 0$
$$x = -2$$
Case 2: $x + 5 = 0$
$$x = -5$$
The zeroes of the polynomial $x^2 + 7x + 10$ are $-2$ and $-5$.
Verification of the relationship between zeroes and coefficients:
Let the zeroes be $\alpha = -2$ and $\beta = -5$.
For a quadratic polynomial $ax^2 + bx + c$, the relationships are:
1. Sum of zeroes: $\alpha + \beta = -\frac{b}{a}$
2. Product of zeroes: $\alpha \times \beta = \frac{c}{a}$
Verify the sum of zeroes:
Sum of zeroes = $\alpha + \beta = -2 + (-5) = -7$
From the coefficients, $-\frac{b}{a} = -\frac{7}{1} = -7$
$$\alpha + \beta = -\frac{b}{a}$$
... (Verified)
Verify the product of zeroes:
Product of zeroes = $\alpha \times \beta = (-2) \times (-5) = 10$}
From the coefficients, $\frac{c}{a} = \frac{10}{1} = 10$
$$\alpha \times \beta = \frac{c}{a}$$
... (Verified)
The relationships between the zeroes and the coefficients are verified.
Final Answer: The zeroes of the polynomial are $-2$ and $-5$. The relationships between the zeroes and coefficients have been verified.
Example 3. Find the zeroes of the polynomial x2 – 3 and verify the relationship between the zeroes and the coefficients.
Answer:
The given quadratic polynomial is $p(x) = x^2 - 3$.
The standard form of a quadratic polynomial is $ax^2 + bx + c$.
Comparing the given polynomial with the standard form, we have the coefficients: $a = 1$, $b = 0$ (since there is no $x$ term), and $c = -3$.
To Find: The zeroes of the polynomial and verify the relationship between zeroes and coefficients.
Solution:
To find the zeroes of the polynomial $p(x)$, we set $p(x) = 0$.
$$x^2 - 3 = 0$$
We can solve for $x^2$:
$$x^2 = 3$$
Taking the square root of both sides:
$$x = \pm \sqrt{3}$$
The zeroes of the polynomial $x^2 - 3$ are $\sqrt{3}$ and $-\sqrt{3}$.
Verification of the relationship between zeroes and coefficients:
Let the zeroes be $\alpha = \sqrt{3}$ and $\beta = -\sqrt{3}$.
For a quadratic polynomial $ax^2 + bx + c$, the relationships are:
1. Sum of zeroes: $\alpha + \beta = -\frac{b}{a}$
2. Product of zeroes: $\alpha \times \beta = \frac{c}{a}$
Verify the sum of zeroes:
Sum of zeroes = $\alpha + \beta = \sqrt{3} + (-\sqrt{3}) = \sqrt{3} - \sqrt{3} = 0$
From the coefficients, $-\frac{b}{a} = -\frac{0}{1} = 0$
$$\alpha + \beta = -\frac{b}{a}$$
... (Verified)
Verify the product of zeroes:
Product of zeroes = $\alpha \times \beta = (\sqrt{3}) \times (-\sqrt{3}) = -(\sqrt{3})^2 = -3$}
From the coefficients, $\frac{c}{a} = \frac{-3}{1} = -3$
$$\alpha \times \beta = \frac{c}{a}$$
... (Verified)
The relationships between the zeroes and the coefficients are verified.
Final Answer: The zeroes of the polynomial are $\sqrt{3}$ and $-\sqrt{3}$. The relationships between the zeroes and coefficients have been verified.
Example 4. Find a quadratic polynomial, the sum and product of whose zeroes are – 3 and 2, respectively.
Answer:
Let the quadratic polynomial be $ax^2 + bx + c$, where $a \neq 0$, and let its zeroes be $\alpha$ and $\beta$.
We know the relationships between the zeroes and the coefficients of a quadratic polynomial:
Sum of zeroes: $\alpha + \beta = -\frac{b}{a}$
Product of zeroes: $\alpha \times \beta = \frac{c}{a}$}
We are given that the sum of the zeroes is $-3$ and the product of the zeroes is $2$.
So, we have:
$\alpha + \beta = -3$
$\alpha \times \beta = 2$
A quadratic polynomial can be written in terms of the sum and product of its zeroes using the formula:
$p(x) = k(x^2 - (\text{Sum of zeroes})x + \text{Product of zeroes})$
$p(x) = k(x^2 - (\alpha + \beta)x + \alpha\beta)$, where $k$ is any non-zero real number.
Substituting the given values for the sum and product of the zeroes:
$p(x) = k(x^2 - (-3)x + 2)$
$p(x) = k(x^2 + 3x + 2)$
Since we are asked to find 'a' quadratic polynomial, we can choose any non-zero value for $k$. The simplest choice is $k=1$.
If we take $k=1$, the polynomial is:
$p(x) = 1 \times (x^2 + 3x + 2)$
$p(x) = x^2 + 3x + 2$
This is one such quadratic polynomial. Other polynomials can be obtained by choosing different values for $k$ (e.g., $2x^2 + 6x + 4$ for $k=2$).
Final Answer: A quadratic polynomial with the given sum and product of zeroes is $x^2 + 3x + 2$.
Example 5. Verify that 3, –1, $-\frac{1}{3}$ are the zeroes of the cubic polynomial p(x) = 3x3 – 5x2 – 11x – 3, and then verify the relationship between the zeroes and the coefficients.
Answer:
The given cubic polynomial is $p(x) = 3x^3 - 5x^2 - 11x - 3$.
The potential zeroes are 3, -1, and $-\frac{1}{3}$.
Step 1: Verify if the given values are zeroes of the polynomial.
A value $x_0$ is a zero of the polynomial $p(x)$ if $p(x_0) = 0$.
For $x = 3$:
$$p(3) = 3(3)^3 - 5(3)^2 - 11(3) - 3$$
$$p(3) = 3(27) - 5(9) - 33 - 3$$
$$p(3) = 81 - 45 - 33 - 3$$
$$p(3) = 81 - (45 + 33 + 3)$$
$$p(3) = 81 - 81$$
$$p(3) = 0$$
Since $p(3) = 0$, 3 is a zero of $p(x)$.
For $x = -1$:
$$p(-1) = 3(-1)^3 - 5(-1)^2 - 11(-1) - 3$$
$$p(-1) = 3(-1) - 5(1) + 11 - 3$$
$$p(-1) = -3 - 5 + 11 - 3$$
$$p(-1) = (-3 - 5 - 3) + 11$$
$$p(-1) = -11 + 11$$
$$p(-1) = 0$$
Since $p(-1) = 0$, -1 is a zero of $p(x)$.
For $x = -\frac{1}{3}$:
$$p\left(-\frac{1}{3}\right) = 3\left(-\frac{1}{3}\right)^3 - 5\left(-\frac{1}{3}\right)^2 - 11\left(-\frac{1}{3}\right) - 3$$
$$p\left(-\frac{1}{3}\right) = 3\left(-\frac{1}{27}\right) - 5\left(\frac{1}{9}\right) - 11\left(-\frac{1}{3}\right) - 3$$
$$p\left(-\frac{1}{3}\right) = -\frac{3}{27} - \frac{5}{9} + \frac{11}{3} - 3$$
$$p\left(-\frac{1}{3}\right) = -\frac{1}{9} - \frac{5}{9} + \frac{11 \times 3}{3 \times 3} - \frac{3 \times 9}{1 \times 9}$$
$$p\left(-\frac{1}{3}\right) = -\frac{1}{9} - \frac{5}{9} + \frac{33}{9} - \frac{27}{9}$$
$$p\left(-\frac{1}{3}\right) = \frac{-1 - 5 + 33 - 27}{9}$$
$$p\left(-\frac{1}{3}\right) = \frac{-6 + 33 - 27}{9}$$
$$p\left(-\frac{1}{3}\right) = \frac{27 - 27}{9}$$
$$p\left(-\frac{1}{3}\right) = \frac{0}{9}$$
$$p\left(-\frac{1}{3}\right) = 0$$
Since $p\left(-\frac{1}{3}\right) = 0$, $-\frac{1}{3}$ is a zero of $p(x)$.
Thus, 3, -1, and $-\frac{1}{3}$ are indeed the zeroes of the polynomial $p(x) = 3x^3 - 5x^2 - 11x - 3$.
Step 2: Identify the coefficients of the polynomial.
The given polynomial is $p(x) = 3x^3 - 5x^2 - 11x - 3$.
Comparing with the standard form of a cubic polynomial $ax^3 + bx^2 + cx + d$, we have:
$a = 3$
$b = -5$
$c = -11$
$d = -3$
Step 3: Verify the relationship between the zeroes and the coefficients.
Let the zeroes be $\alpha = 3$, $\beta = -1$, and $\gamma = -\frac{1}{3}$.
The relationships for a cubic polynomial $ax^3 + bx^2 + cx + d$ are:
1. Sum of zeroes: $\alpha + \beta + \gamma = -\frac{b}{a}$
2. Sum of the product of zeroes taken two at a time: $\alpha\beta + \beta\gamma + \gamma\alpha = \frac{c}{a}$
3. Product of zeroes: $\alpha\beta\gamma = -\frac{d}{a}$
Verify the sum of zeroes:
Sum of zeroes from the given values:
$$\alpha + \beta + \gamma = 3 + (-1) + \left(-\frac{1}{3}\right) = 3 - 1 - \frac{1}{3} = 2 - \frac{1}{3} = \frac{6 - 1}{3} = \frac{5}{3}$$
Sum of zeroes from the coefficients:
$$-\frac{b}{a} = -\frac{(-5)}{3} = \frac{5}{3}$$
The sum of zeroes matches: $\frac{5}{3} = \frac{5}{3}$.
Verify the sum of the product of zeroes taken two at a time:
Sum of product of zeroes from the given values:
$$\alpha\beta + \beta\gamma + \gamma\alpha = (3)(-1) + (-1)\left(-\frac{1}{3}\right) + \left(-\frac{1}{3}\right)(3)$$
$$= -3 + \frac{1}{3} - 1$$
$$= -4 + \frac{1}{3}$$
$$= \frac{-12 + 1}{3} = -\frac{11}{3}$$
Sum of product of zeroes from the coefficients:
$$\frac{c}{a} = \frac{-11}{3} = -\frac{11}{3}$$
The sum of the product of zeroes taken two at a time matches: $-\frac{11}{3} = -\frac{11}{3}$.
Verify the product of zeroes:
Product of zeroes from the given values:
$$\alpha\beta\gamma = (3)(-1)\left(-\frac{1}{3}\right)$$
$$= 3 \times (-1) \times \left(-\frac{1}{3}\right)$$
$$= -3 \times \left(-\frac{1}{3}\right)$$
$$= 1$$
Product of zeroes from the coefficients:
$$-\frac{d}{a} = -\frac{(-3)}{3} = \frac{3}{3} = 1$$
The product of zeroes matches: $1 = 1$.
All the relationships between the zeroes and the coefficients are verified.
Final Answer: The given values 3, -1, and $-\frac{1}{3}$ are verified as the zeroes of the polynomial. The relationships between the zeroes and the coefficients have also been verified.
Exercise 2.2
Question 1. Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
(i) x2 – 2x – 8
(ii) 4s2 – 4s + 1
(iii) 6x2 – 3 – 7x
(iv) 4u2 + 8u
(v) t2 – 15
(vi) 3x2 – x – 4
Answer:
We will find the zeroes for each quadratic polynomial and verify the relationship between the zeroes and the coefficients using the formulas: Sum of zeroes $= -\frac{b}{a}$ and Product of zeroes $= \frac{c}{a}$.
(i) $x^2 – 2x – 8$
The polynomial is $p(x) = x^2 - 2x - 8$. Comparing with $ax^2 + bx + c$, we have $a=1$, $b=-2$, $c=-8$.
To find the zeroes, set $p(x) = 0$:
$$x^2 - 2x - 8 = 0$$
Factor the quadratic expression. We need two numbers that multiply to -8 and add to -2. These numbers are 2 and -4.
$$x^2 + 2x - 4x - 8 = 0$$
$$x(x + 2) - 4(x + 2) = 0$$
$$(x + 2)(x - 4) = 0$$
Setting each factor to zero gives the zeroes:
$x + 2 = 0 \implies x = -2$
$x - 4 = 0 \implies x = 4$
The zeroes are $\alpha = -2$ and $\beta = 4$.
Verification:
Sum of zeroes: $\alpha + \beta = -2 + 4 = 2$
From coefficients: $-\frac{b}{a} = -\frac{(-2)}{1} = 2$
$\alpha + \beta = -\frac{b}{a}$
(Verified)
Product of zeroes: $\alpha \times \beta = (-2) \times 4 = -8$
From coefficients: $\frac{c}{a} = \frac{-8}{1} = -8$
$\alpha \times \beta = \frac{c}{a}$
(Verified)
(ii) $4s^2 – 4s + 1$
The polynomial is $p(s) = 4s^2 - 4s + 1$. Comparing with $as^2 + bs + c$, we have $a=4$, $b=-4$, $c=1$.
To find the zeroes, set $p(s) = 0$:
$$4s^2 - 4s + 1 = 0$$
Factor the quadratic expression. This is a perfect square trinomial: $(2s - 1)^2$.
$$(2s - 1)^2 = 0$$
Setting the factor to zero gives the zeroes:
$2s - 1 = 0 \implies 2s = 1 \implies s = \frac{1}{2}$
The polynomial has a repeated zero at $s = \frac{1}{2}$. So, the zeroes are $\alpha = \frac{1}{2}$ and $\beta = \frac{1}{2}$.
Verification:
Sum of zeroes: $\alpha + \beta = \frac{1}{2} + \frac{1}{2} = 1$
From coefficients: $-\frac{b}{a} = -\frac{(-4)}{4} = \frac{4}{4} = 1$
$\alpha + \beta = -\frac{b}{a}$
(Verified)
Product of zeroes: $\alpha \times \beta = \frac{1}{2} \times \frac{1}{2} = \frac{1}{4}$
From coefficients: $\frac{c}{a} = \frac{1}{4}$
$\alpha \times \beta = \frac{c}{a}$
(Verified)
(iii) $6x^2 – 3 – 7x$
Rearrange the polynomial in standard form: $p(x) = 6x^2 - 7x - 3$. Comparing with $ax^2 + bx + c$, we have $a=6$, $b=-7$, $c=-3$.
To find the zeroes, set $p(x) = 0$:
$$6x^2 - 7x - 3 = 0$$
Factor the quadratic expression. We look for two numbers that multiply to $a \times c = 6 \times (-3) = -18$ and add to $b = -7$. These numbers are 2 and -9.
Rewrite the middle term $-7x$ as $2x - 9x$:
$$6x^2 + 2x - 9x - 3 = 0$$
Group the terms and factor:
$$2x(3x + 1) - 3(3x + 1) = 0$$
$$(3x + 1)(2x - 3) = 0$$
Setting each factor to zero gives the zeroes:
$3x + 1 = 0 \implies 3x = -1 \implies x = -\frac{1}{3}$
$2x - 3 = 0 \implies 2x = 3 \implies x = \frac{3}{2}$
The zeroes are $\alpha = -\frac{1}{3}$ and $\beta = \frac{3}{2}$.
Verification:
Sum of zeroes: $\alpha + \beta = -\frac{1}{3} + \frac{3}{2} = \frac{-1 \times 2 + 3 \times 3}{6} = \frac{-2 + 9}{6} = \frac{7}{6}$
From coefficients: $-\frac{b}{a} = -\frac{(-7)}{6} = \frac{7}{6}$
$\alpha + \beta = -\frac{b}{a}$
(Verified)
Product of zeroes: $\alpha \times \beta = \left(-\frac{1}{3}\right) \times \left(\frac{3}{2}\right) = -\frac{1 \times \cancel{3}}{ \cancel{3} \times 2} = -\frac{1}{2}$
From coefficients: $\frac{c}{a} = \frac{-3}{6} = -\frac{1}{2}$
$\alpha \times \beta = \frac{c}{a}$
(Verified)
(iv) $4u^2 + 8u$
The polynomial is $p(u) = 4u^2 + 8u$. Comparing with $au^2 + bu + c$, we have $a=4$, $b=8$, $c=0$.
To find the zeroes, set $p(u) = 0$:
$$4u^2 + 8u = 0$$
Factor out the common term $4u$:
$$4u(u + 2) = 0$$
Setting each factor to zero gives the zeroes:
$4u = 0 \implies u = 0$
$u + 2 = 0 \implies u = -2$
The zeroes are $\alpha = 0$ and $\beta = -2$.
Verification:
Sum of zeroes: $\alpha + \beta = 0 + (-2) = -2$
From coefficients: $-\frac{b}{a} = -\frac{8}{4} = -2$
$\alpha + \beta = -\frac{b}{a}$
(Verified)
Product of zeroes: $\alpha \times \beta = 0 \times (-2) = 0$}
From coefficients: $\frac{c}{a} = \frac{0}{4} = 0$
$\alpha \times \beta = \frac{c}{a}$
(Verified)
(v) $t^2 – 15$
The polynomial is $p(t) = t^2 - 15$. Comparing with $at^2 + bt + c$, we have $a=1$, $b=0$, $c=-15$.
To find the zeroes, set $p(t) = 0$:
$$t^2 - 15 = 0$$
$$t^2 = 15$$
$$t = \pm \sqrt{15}$$
The zeroes are $\alpha = \sqrt{15}$ and $\beta = -\sqrt{15}$.
Verification:
Sum of zeroes: $\alpha + \beta = \sqrt{15} + (-\sqrt{15}) = 0$
From coefficients: $-\frac{b}{a} = -\frac{0}{1} = 0$
$\alpha + \beta = -\frac{b}{a}$
(Verified)
Product of zeroes: $\alpha \times \beta = (\sqrt{15}) \times (-\sqrt{15}) = -(\sqrt{15})^2 = -15$}
From coefficients: $\frac{c}{a} = \frac{-15}{1} = -15$
$\alpha \times \beta = \frac{c}{a}$
(Verified)
(vi) $3x^2 – x – 4$
The polynomial is $p(x) = 3x^2 - x - 4$. Comparing with $ax^2 + bx + c$, we have $a=3$, $b=-1$, $c=-4$.
To find the zeroes, set $p(x) = 0$:
$$3x^2 - x - 4 = 0$$
Factor the quadratic expression. We look for two numbers that multiply to $a \times c = 3 \times (-4) = -12$ and add to $b = -1$. These numbers are 3 and -4.
Rewrite the middle term $-x$ as $3x - 4x$:
$$3x^2 + 3x - 4x - 4 = 0$$
Group the terms and factor:
$$3x(x + 1) - 4(x + 1) = 0$$
$$(x + 1)(3x - 4) = 0$$
Setting each factor to zero gives the zeroes:
$x + 1 = 0 \implies x = -1$}
$3x - 4 = 0 \implies 3x = 4 \implies x = \frac{4}{3}$
The zeroes are $\alpha = -1$ and $\beta = \frac{4}{3}$.
Verification:
Sum of zeroes: $\alpha + \beta = -1 + \frac{4}{3} = \frac{-3}{3} + \frac{4}{3} = \frac{-3+4}{3} = \frac{1}{3}$
From coefficients: $-\frac{b}{a} = -\frac{(-1)}{3} = \frac{1}{3}$
$\alpha + \beta = -\frac{b}{a}$
(Verified)
Product of zeroes: $\alpha \times \beta = (-1) \times \left(\frac{4}{3}\right) = -\frac{4}{3}$
From coefficients: $\frac{c}{a} = \frac{-4}{3} = -\frac{4}{3}$
$\alpha \times \beta = \frac{c}{a}$
(Verified)
Question 2. Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.
(i) $\frac{1}{4}$ , −1
(ii) $\sqrt{2}$ , $\frac{1}{3}$
(iii) 0 , $\sqrt{5}$
(iv) 1 , 1
(v) $-\frac{1}{4}$ , $\frac{1}{4}$
(vi) 4, 1
Answer:
Let the sum of the zeroes of a quadratic polynomial be $S$ and the product of the zeroes be $P$. A quadratic polynomial with sum of zeroes $S$ and product of zeroes $P$ can be written as:
$$p(x) = k(x^2 - Sx + P)$$
where $k$ is any non-zero real number.
We will use this formula for each part, taking $k=1$ for simplicity to find 'a' quadratic polynomial.
(i) Sum = $\frac{1}{4}$, Product = $-1$
Here, $S = \frac{1}{4}$ and $P = -1$.
Using the formula with $k=1$:
$$p(x) = x^2 - \left(\frac{1}{4}\right)x + (-1)$$
$$p(x) = x^2 - \frac{1}{4}x - 1$$
To get integer coefficients, we can take $k=4$.
$$p(x) = 4\left(x^2 - \frac{1}{4}x - 1\right) = 4x^2 - x - 4$$
A quadratic polynomial is $4x^2 - x - 4$.
(ii) Sum = $\sqrt{2}$, Product = $\frac{1}{3}$
Here, $S = \sqrt{2}$ and $P = \frac{1}{3}$.
Using the formula with $k=1$:
$$p(x) = x^2 - (\sqrt{2})x + \frac{1}{3}$$
$$p(x) = x^2 - \sqrt{2}x + \frac{1}{3}$$
To clear the fraction, we can take $k=3$.
$$p(x) = 3\left(x^2 - \sqrt{2}x + \frac{1}{3}\right) = 3x^2 - 3\sqrt{2}x + 1$$
A quadratic polynomial is $3x^2 - 3\sqrt{2}x + 1$.
(iii) Sum = 0, Product = $\sqrt{5}$
Here, $S = 0$ and $P = \sqrt{5}$.
Using the formula with $k=1$:
$$p(x) = x^2 - (0)x + \sqrt{5}$$
$$p(x) = x^2 + \sqrt{5}$$
A quadratic polynomial is $x^2 + \sqrt{5}$.
(iv) Sum = 1, Product = 1
Here, $S = 1$ and $P = 1$.
Using the formula with $k=1$:
$$p(x) = x^2 - (1)x + 1$$
$$p(x) = x^2 - x + 1$$
A quadratic polynomial is $x^2 - x + 1$.
(v) Sum = $-\frac{1}{4}$, Product = $\frac{1}{4}$
Here, $S = -\frac{1}{4}$ and $P = \frac{1}{4}$.
Using the formula with $k=1$:
$$p(x) = x^2 - \left(-\frac{1}{4}\right)x + \frac{1}{4}$$
$$p(x) = x^2 + \frac{1}{4}x + \frac{1}{4}$$
To clear the fractions, we can take $k=4$.
$$p(x) = 4\left(x^2 + \frac{1}{4}x + \frac{1}{4}\right) = 4x^2 + x + 1$$
A quadratic polynomial is $4x^2 + x + 1$.
(vi) Sum = 4, Product = 1
Here, $S = 4$ and $P = 1$.
Using the formula with $k=1$:
$$p(x) = x^2 - (4)x + 1$$
$$p(x) = x^2 - 4x + 1$$
A quadratic polynomial is $x^2 - 4x + 1$.
Example 6 to 9 (Before Exercise 2.3)
Example 6. Divide 2x2 + 3x + 1 by x + 2.
Answer:
We need to divide the polynomial $p(x) = 2x^2 + 3x + 1$ by the polynomial $g(x) = x + 2$ using polynomial long division.
We perform the long division as follows:
$$ \begin{array}{r} 2x - 1\phantom{)} \\ x+2{\overline{\smash{\big)}\,2x^2+3x+1\phantom{)}}} \\ \underline{-~\phantom{()}(2x^2+4x)\phantom{)}} \\ -x+1\phantom{)} \\ \underline{-~\phantom{()}(-x-2)} \\ 3\phantom{)} \end{array} $$From the polynomial long division, we find:
Quotient, $q(x) = 2x - 1$
Remainder, $r(x) = 3$
According to the Division Algorithm for Polynomials, we can write:
$p(x) = g(x) \times q(x) + r(x)$
Substituting the polynomials we have:
$$2x^2 + 3x + 1 = (x + 2)(2x - 1) + 3$$
Let's verify this:
$$(x + 2)(2x - 1) + 3 = x(2x - 1) + 2(2x - 1) + 3$$
$$= (2x^2 - x) + (4x - 2) + 3$$
$$= 2x^2 + (-x + 4x) + (-2 + 3)$$
$$= 2x^2 + 3x + 1$$
The verification confirms our division is correct.
Final Answer:
The quotient is $2x - 1$ and the remainder is 3.
Example 7. Divide 3x3 + x2 + 2x + 5 by 1 + 2x + x2.
Answer:
We need to divide the polynomial $p(x) = 3x^3 + x^2 + 2x + 5$ by the polynomial $g(x) = 1 + 2x + x^2$.
First, arrange the divisor in descending powers of $x$: $g(x) = x^2 + 2x + 1$.
We perform the polynomial long division:
$$ \begin{array}{r} 3x - 5\phantom{)} \\ x^2+2x+1{\overline{\smash{\big)}\,3x^3+x^2+2x+5\phantom{)}}} \\ \underline{-~\phantom{()}(3x^3+6x^2+3x)\phantom{)}} \\ -5x^2-x+5\phantom{)} \\ \underline{-~\phantom{()}(-5x^2-10x-5)} \\ 9x+10\phantom{)} \end{array} $$From the polynomial long division, we find:
Quotient, $q(x) = 3x - 5$
Remainder, $r(x) = 9x + 10$}
According to the Division Algorithm for Polynomials, we can write:
$p(x) = g(x) \times q(x) + r(x)$
Substituting the polynomials we have:
$$3x^3 + x^2 + 2x + 5 = (x^2 + 2x + 1)(3x - 5) + (9x + 10)$$
Let's verify this:
$$(x^2 + 2x + 1)(3x - 5) + (9x + 10) = x^2(3x - 5) + 2x(3x - 5) + 1(3x - 5) + 9x + 10$$
$$= (3x^3 - 5x^2) + (6x^2 - 10x) + (3x - 5) + 9x + 10$$
$$= 3x^3 + (-5x^2 + 6x^2) + (-10x + 3x + 9x) + (-5 + 10)$$
$$= 3x^3 + x^2 + (-7x + 9x) + 5$$
$$= 3x^3 + x^2 + 2x + 5$$
The verification confirms our division is correct.
Final Answer:
The quotient is $3x - 5$ and the remainder is $9x + 10$.
Example 8. Divide 3x2 – x3 – 3x + 5 by x – 1 – x2 , and verify the division algorithm.
Answer:
We need to divide the polynomial $p(x) = 3x^2 - x^3 - 3x + 5$ by the polynomial $g(x) = x - 1 - x^2$, and then verify the division algorithm.
First, arrange both the dividend and the divisor in descending powers of $x$:
Dividend: $p(x) = -x^3 + 3x^2 - 3x + 5$
Divisor: $g(x) = -x^2 + x - 1$
Now, perform the polynomial long division:
$$ \begin{array}{r} x - 2\phantom{)} \\ -x^2+x-1{\overline{\smash{\big)}\,-x^3+3x^2-3x+5\phantom{)}}} \\ \underline{-~\phantom{()}(-x^3+x^2-x)\phantom{-b)}} \\ 0+2x^2-2x+5\phantom{)} \\ \underline{-~\phantom{()}(2x^2-2x+2)} \\ 0+0+3\phantom{)} \end{array} $$From the polynomial long division, we find:
Quotient, $q(x) = x - 2$
Remainder, $r(x) = 3$}
Verification of the division algorithm:
The Division Algorithm for Polynomials states that $p(x) = g(x) \times q(x) + r(x)$.
Let's calculate $g(x) \times q(x) + r(x)$ using our results:
$$g(x) \times q(x) + r(x) = (-x^2 + x - 1) \times (x - 2) + 3$$
Multiply the polynomials $g(x)$ and $q(x)$:
$$(-x^2 + x - 1)(x - 2) = -x^2(x - 2) + x(x - 2) - 1(x - 2)$$
$$= (-x^3 + 2x^2) + (x^2 - 2x) - (x - 2)$$
$$= -x^3 + 2x^2 + x^2 - 2x - x + 2$$
Combine like terms:
$$= -x^3 + (2x^2 + x^2) + (-2x - x) + 2$$
$$= -x^3 + 3x^2 - 3x + 2$$
Now, add the remainder $r(x) = 3$:
$$(-x^3 + 3x^2 - 3x + 2) + 3$$
$$= -x^3 + 3x^2 - 3x + (2 + 3)$$
$$= -x^3 + 3x^2 - 3x + 5$$
This result is equal to the dividend $p(x) = -x^3 + 3x^2 - 3x + 5$.
So, we have $p(x) = g(x) \times q(x) + r(x)$ verified.
Final Answer:
The quotient is $x - 2$ and the remainder is 3.
The division algorithm $p(x) = g(x) \times q(x) + r(x)$ is verified as $-x^3 + 3x^2 - 3x + 5 = (-x^2 + x - 1)(x - 2) + 3$.
Example 9. Find all the zeroes of 2x4 – 3x3 – 3x2 + 6x – 2, if you know that two of its zeroes are $\sqrt{2}$ and $-\sqrt{2}$ .
Answer:
The given polynomial is $p(x) = 2x^4 – 3x^3 – 3x^2 + 6x – 2$.
We are given that two of the zeroes are $\sqrt{2}$ and $-\sqrt{2}$.
If $a$ is a zero of a polynomial, then $(x - a)$ is a factor of the polynomial.
Since $\sqrt{2}$ and $-\sqrt{2}$ are zeroes of $p(x)$, the factors $(x - \sqrt{2})$ and $(x - (-\sqrt{2})) = (x + \sqrt{2})$ are factors of $p(x)$.
The product of these two factors is also a factor of $p(x)$.
Product of factors = $(x - \sqrt{2})(x + \sqrt{2}) = x^2 - (\sqrt{2})^2 = x^2 - 2$.
So, $(x^2 - 2)$ is a factor of the polynomial $p(x)$.
Since $(x^2 - 2)$ is a factor of $p(x)$, we can find the other factors by dividing $p(x)$ by $(x^2 - 2)$ using polynomial long division.
We divide $2x^4 – 3x^3 – 3x^2 + 6x – 2$ by $x^2 - 2$. We can write the divisor as $x^2 + 0x - 2$ for convenience in long division.
$$ \begin{array}{r} 2x^2 -3x + 1\phantom{)} \\ x^2+0x-2{\overline{\smash{\big)}\,2x^4-3x^3-3x^2+6x-2\phantom{)}}} \\ \underline{-~\phantom{()}(2x^4+0x^3-4x^2)\phantom{-b)}} \\ -3x^3+x^2+6x-2\phantom{)} \\ \underline{-~\phantom{()}(-3x^3+0x^2+6x)} \\ x^2+0x-2\phantom{)} \\ \underline{-~\phantom{()}(x^2+0x-2)} \\ 0\phantom{)} \end{array} $$The remainder is 0, which confirms that $x^2 - 2$ is a factor.
The quotient is $q(x) = 2x^2 - 3x + 1$.
The remaining zeroes of $p(x)$ are the zeroes of the quotient polynomial $2x^2 - 3x + 1$.
To find the zeroes of $2x^2 - 3x + 1$, we set the polynomial equal to zero:
$$2x^2 - 3x + 1 = 0$$
We can factor this quadratic equation. We look for two numbers that multiply to $2 \times 1 = 2$ and add to $-3$. These numbers are $-1$ and $-2$.
Rewrite the middle term $-3x$ as $-x - 2x$:
$$2x^2 - x - 2x + 1 = 0$$
Group the terms and factor:
$$x(2x - 1) - 1(2x - 1) = 0$$
Factor out the common binomial factor $(2x - 1)$:
$$(2x - 1)(x - 1) = 0$$
Setting each factor to zero gives the remaining zeroes:
Case 1: $2x - 1 = 0$
$$2x = 1 \implies x = \frac{1}{2}$$
Case 2: $x - 1 = 0$
$$x = 1$$
So, the other two zeroes are $\frac{1}{2}$ and $1$.
The polynomial $p(x)$ is a quartic polynomial (degree 4), so it has exactly 4 zeroes (counting multiplicity).
Final Answer: The zeroes of the polynomial $2x^4 – 3x^3 – 3x^2 + 6x – 2$ are $\sqrt{2}$, $-\sqrt{2}$, $\frac{1}{2}$, and $1$.
Exercise 2.3
Question 1. Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following:
(i) p(x) = x3 – 3x2 + 5x – 3, g(x) = x2 – 2
(ii) p(x) = x4 – 3x2 + 4x + 5, g(x) = x2 + 1 – x
(iii) p(x) = x4 – 5x + 6, g(x) = 2 – x2
Answer:
We will perform polynomial long division for each given pair of polynomials $(p(x), g(x))$ to find the quotient and remainder.
(i) $p(x) = x^3 – 3x^2 + 5x – 3$, $g(x) = x^2 – 2$
We divide $x^3 - 3x^2 + 5x - 3$ by $x^2 - 2$. We can write the divisor as $x^2 + 0x - 2$ for convenience in long division.
$$ \begin{array}{r} x - 3\phantom{)} \\ x^2+0x-2{\overline{\smash{\big)}\,x^3-3x^2+5x-3\phantom{)}}} \\ \underline{-~\phantom{()}(x^3+0x^2-2x)\phantom{-b)}} \\ -3x^2+7x-3\phantom{)} \\ \underline{-~\phantom{()}(-3x^2+0x+6)} \\ 7x-9\phantom{)} \end{array} $$From the division:
The quotient is $q(x) = x - 3$.
The remainder is $r(x) = 7x - 9$.
(ii) $p(x) = x^4 – 3x^2 + 4x + 5$, $g(x) = x^2 + 1 – x$
Arrange the polynomials in descending powers of $x$.
Dividend: $p(x) = x^4 + 0x^3 - 3x^2 + 4x + 5$
Divisor: $g(x) = x^2 - x + 1$
We divide $x^4 - 3x^2 + 4x + 5$ by $x^2 - x + 1$.
$$ \begin{array}{r} x^2+x-3\phantom{)} \\ x^2-x+1{\overline{\smash{\big)}\,x^4+0x^3-3x^2+4x+5\phantom{)}}} \\ \underline{-~\phantom{()}(x^4-x^3+x^2)\phantom{-b)}} \\ x^3-4x^2+4x+5\phantom{)} \\ \underline{-~\phantom{()}(x^3-x^2+x)\phantom{-b)}} \\ -3x^2+3x+5\phantom{)} \\ \underline{-~\phantom{()}(-3x^2+3x-3)} \\ 8\phantom{)} \end{array} $$From the division:
The quotient is $q(x) = x^2 + x - 3$.
The remainder is $r(x) = 8$.
(iii) $p(x) = x^4 – 5x + 6$, $g(x) = 2 – x^2$
Arrange the polynomials in descending powers of $x$.
Dividend: $p(x) = x^4 + 0x^3 + 0x^2 - 5x + 6$
Divisor: $g(x) = -x^2 + 2$. We can write this as $-x^2 + 0x + 2$ for convenience.
We divide $x^4 - 5x + 6$ by $-x^2 + 2$.
$$ \begin{array}{r} -x^2 - 2\phantom{)} \\ -x^2+0x+2{\overline{\smash{\big)}\,x^4+0x^3+0x^2-5x+6\phantom{)}}} \\ \underline{-~\phantom{()}(x^4+0x^3-2x^2)\phantom{-b)}} \\ 0+0+2x^2-5x+6\phantom{)} \\ \underline{-~\phantom{()}(2x^2+0x-4)} \\ -5x+10\phantom{)} \end{array} $$From the division:
The quotient is $q(x) = -x^2 - 2$.
The remainder is $r(x) = -5x + 10$.
Question 2. Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial:
(i) t2 – 3, 2t4 + 3t3 – 2t2 – 9t – 12
(ii) x2 + 3x + 1, 3x4 + 5x3 – 7x2 + 2x + 2
(iii) x3 – 3x + 1, x5 – 4x3 + x2 + 3x + 1
Answer:
To check if the first polynomial $g(x)$ is a factor of the second polynomial $p(x)$, we divide $p(x)$ by $g(x)$. If the remainder is 0, then $g(x)$ is a factor of $p(x)$.
(i) $p(t) = 2t^4 + 3t^3 – 2t^2 – 9t – 12$, $g(t) = t^2 – 3$
We divide $2t^4 + 3t^3 – 2t^2 – 9t – 12$ by $t^2 – 3$. We can write $g(t)$ as $t^2 + 0t - 3$ for the long division.
$$ \begin{array}{r} 2t^2 + 3t + 4\phantom{)} \\ t^2+0t-3{\overline{\smash{\big)}\,2t^4+3t^3-2t^2-9t-12\phantom{)}}} \\ \underline{-~\phantom{()}(2t^4+0t^3-6t^2)\phantom{-b)}} \\ 3t^3+4t^2-9t-12\phantom{)} \\ \underline{-~\phantom{()}(3t^3+0t^2-9t)} \\ 4t^2+0t-12\phantom{)} \\ \underline{-~\phantom{()}(4t^2+0t-12)} \\ 0\phantom{)} \end{array} $$The remainder is 0.
Since the remainder is 0, the first polynomial $t^2 - 3$ is a factor of the second polynomial $2t^4 + 3t^3 – 2t^2 – 9t – 12$.
(ii) $p(x) = 3x^4 + 5x^3 – 7x^2 + 2x + 2$, $g(x) = x^2 + 3x + 1$
We divide $3x^4 + 5x^3 – 7x^2 + 2x + 2$ by $x^2 + 3x + 1$.
$$ \begin{array}{r} 3x^2 - 4x + 2\phantom{)} \\ x^2+3x+1{\overline{\smash{\big)}\,3x^4+5x^3-7x^2+2x+2\phantom{)}}} \\ \underline{-~\phantom{()}(3x^4+9x^3+3x^2)\phantom{-b)}} \\ -4x^3-10x^2+2x+2\phantom{)} \\ \underline{-~\phantom{()}(-4x^3-12x^2-4x)} \\ 2x^2+6x+2\phantom{)} \\ \underline{-~\phantom{()}(2x^2+6x+2)} \\ 0\phantom{)} \end{array} $$The remainder is 0.
Since the remainder is 0, the first polynomial $x^2 + 3x + 1$ is a factor of the second polynomial $3x^4 + 5x^3 – 7x^2 + 2x + 2$.
(iii) $p(x) = x^5 – 4x^3 + x^2 + 3x + 1$, $g(x) = x^3 – 3x + 1$
Arrange the polynomials in descending powers of $x$.
Dividend: $p(x) = x^5 + 0x^4 - 4x^3 + x^2 + 3x + 1$
Divisor: $g(x) = x^3 + 0x^2 - 3x + 1$
We divide $x^5 – 4x^3 + x^2 + 3x + 1$ by $x^3 – 3x + 1$.
$$ \begin{array}{r} x^2 - 1\phantom{)} \\ x^3+0x^2-3x+1{\overline{\smash{\big)}\,x^5+0x^4-4x^3+x^2+3x+1\phantom{)}}} \\ \underline{-~\phantom{()}(x^5+0x^4-3x^3+x^2)\phantom{-b)}} \\ -x^3+0x^2+3x+1\phantom{)} \\ \underline{-~\phantom{()}(-x^3+0x^2+3x-1)} \\ 0+0+0+2\phantom{)} \end{array} $$The remainder is 2.
Since the remainder is not 0, the first polynomial $x^3 – 3x + 1$ is not a factor of the second polynomial $x^5 – 4x^3 + x^2 + 3x + 1$.
Question 3. Obtain all other zeroes of 3x4 + 6x3 – 2x2 – 10x – 5, if two of its zeroes are $\sqrt{\frac{5}{3}}$ and $-\sqrt{\frac{5}{3}}$
Answer:
Let the given polynomial be $p(x) = 3x^4 + 6x^3 – 2x^2 – 10x – 5$.
We are given that two of the zeroes of $p(x)$ are $\sqrt{\frac{5}{3}}$ and $-\sqrt{\frac{5}{3}}$.
If $a$ is a zero of a polynomial, then $(x - a)$ is a factor of the polynomial.
Since $\sqrt{\frac{5}{3}}$ is a zero, $(x - \sqrt{\frac{5}{3}})$ is a factor of $p(x)$.
Since $-\sqrt{\frac{5}{3}}$ is a zero, $(x - (-\sqrt{\frac{5}{3}})) = (x + \sqrt{\frac{5}{3}})$ is a factor of $p(x)$.
Since $(x - \sqrt{\frac{5}{3}})$ and $(x + \sqrt{\frac{5}{3}})$ are factors, their product is also a factor of $p(x)$.
Product of factors $= \left(x - \sqrt{\frac{5}{3}}\right)\left(x + \sqrt{\frac{5}{3}}\right)$
Using the identity $(a-b)(a+b) = a^2 - b^2$:
Product $= x^2 - \left(\sqrt{\frac{5}{3}}\right)^2 = x^2 - \frac{5}{3}$.
So, $\left(x^2 - \frac{5}{3}\right)$ is a factor of $p(x)$.
Since $\left(x^2 - \frac{5}{3}\right)$ is a factor of $p(x)$, any non-zero multiple of it is also related to the factorization. The polynomial $3\left(x^2 - \frac{5}{3}\right) = 3x^2 - 5$ is also a factor of $p(x)$ because the coefficients of $p(x)$ are integers and the leading coefficient is a multiple of the coefficients derived from the factor.
We can find the other factors of $p(x)$ by dividing $p(x)$ by $(3x^2 - 5)$ using polynomial long division.
Divide $3x^4 + 6x^3 – 2x^2 – 10x – 5$ by $3x^2 - 5$. We can write the divisor as $3x^2 + 0x - 5$ for convenience.
$$ \begin{array}{r} x^2+2x+1\phantom{)} \\ 3x^2+0x-5{\overline{\smash{\big)}\,3x^4+6x^3-2x^2-10x-5\phantom{)}}} \\ \underline{-~\phantom{()}(3x^4+0x^3-5x^2)\phantom{-b)}} \\ 6x^3+3x^2-10x-5\phantom{)} \\ \underline{-~\phantom{()}(6x^3+0x^2-10x)} \\ 3x^2+0x-5\phantom{)} \\ \underline{-~\phantom{()}(3x^2+0x-5)} \\ 0\phantom{)} \end{array} $$The remainder is 0, which confirms that $3x^2 - 5$ is a factor.
The quotient is $q(x) = x^2 + 2x + 1$.
The remaining zeroes of $p(x)$ are the zeroes of the quotient polynomial $x^2 + 2x + 1$.
To find the zeroes of $x^2 + 2x + 1$, we set the polynomial equal to zero:
$$x^2 + 2x + 1 = 0$$
Factor this quadratic equation. This is a perfect square trinomial:
$$(x + 1)^2 = 0$$
Setting the factor to zero gives the remaining zeroes:
$x + 1 = 0 \implies x = -1$
Since the factor is squared, the zero $x=-1$ has a multiplicity of 2.
The given polynomial $p(x)$ is of degree 4, so it has exactly 4 zeroes (counting multiplicity).
The given zeroes are $\sqrt{\frac{5}{3}}$ and $-\sqrt{\frac{5}{3}}$.
The zeroes obtained from the quotient are -1 and -1.
Final Answer: The other zeroes of the polynomial $3x^4 + 6x^3 – 2x^2 – 10x – 5$ are $-1$ and $-1$.
Question 4. On dividing x3 – 3x2 + x + 2 by a polynomial g(x), the quotient and remainder were x – 2 and –2x + 4, respectively. Find g(x).
Answer:
Given:
Dividend $p(x) = x^3 – 3x^2 + x + 2$
Divisor $g(x)$ (unknown)
Quotient $q(x) = x – 2$
Remainder $r(x) = –2x + 4$
To Find: The polynomial $g(x)$.
Solution:
According to the Division Algorithm for Polynomials, we have the relationship:
$$p(x) = g(x) \times q(x) + r(x)$$$
... (i)
We need to find $g(x)$. We can rearrange the formula (i) to isolate the term containing $g(x)$:
$$p(x) - r(x) = g(x) \times q(x)$$$
To find $g(x)$, we divide $p(x) - r(x)$ by $q(x)$:
$$g(x) = \frac{p(x) - r(x)}{q(x)}$$$
... (ii)
First, let's calculate $p(x) - r(x)$:
$$p(x) - r(x) = (x^3 – 3x^2 + x + 2) - (–2x + 4)$$$
$$p(x) - r(x) = x^3 – 3x^2 + x + 2 + 2x - 4$$
Combine the like terms:
$$p(x) - r(x) = x^3 – 3x^2 + (x + 2x) + (2 - 4)$$$
$$p(x) - r(x) = x^3 – 3x^2 + 3x - 2$$
Now, we need to divide the polynomial $x^3 – 3x^2 + 3x - 2$ by $q(x) = x - 2$ to find $g(x)$. We perform polynomial long division.
Divide $x^3 – 3x^2 + 3x - 2$ by $x - 2$:
$$ \begin{array}{r} x^2 - x + 1\phantom{)} \\ x-2{\overline{\smash{\big)}\,x^3-3x^2+3x-2\phantom{)}}} \\ \underline{-~\phantom{()}(x^3-2x^2)\phantom{-b)}} \\ -x^2+3x-2\phantom{)} \\ \underline{-~\phantom{()}(-x^2+2x)} \\ x-2\phantom{)} \\ \underline{-~\phantom{()}(x-2)} \\ 0\phantom{)} \end{array} $$The result of the division is the quotient $x^2 - x + 1$ with a remainder of 0.
Therefore, $g(x) = x^2 - x + 1$.
Final Answer: The polynomial $g(x)$ is $x^2 - x + 1$.
Question 5. Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and
(i) deg p(x) = deg q(x)
(ii) deg q(x) = deg r(x)
(iii) deg r(x) = 0
Answer:
According to the Division Algorithm for Polynomials, for any polynomials $p(x)$ and $g(x)$ with $g(x) \neq 0$, there exist unique polynomials $q(x)$ and $r(x)$ such that $p(x) = g(x) \times q(x) + r(x)$, where $r(x) = 0$ or $\text{deg } r(x) < \text{deg } g(x)$.
We will provide an example for each case satisfying the given conditions.
(i) deg p(x) = deg q(x)
This condition implies that the degree of the divisor $g(x)$ must be 0. A polynomial of degree 0 is a non-zero constant.
Let $p(x) = x^2 + x + 1$. $\text{deg } p(x) = 2$.
Let $g(x) = 5$ (a non-zero constant). $\text{deg } g(x) = 0$.
Dividing $p(x)$ by $g(x)$:
$$p(x) = g(x) \times q(x) + r(x)$$
$$x^2 + x + 1 = 5 \times q(x) + r(x)$$
The quotient $q(x)$ is $\frac{1}{5}(x^2 + x + 1) = \frac{1}{5}x^2 + \frac{1}{5}x + \frac{1}{5}$, and the remainder $r(x)$ is 0.
Here, $\text{deg } q(x) = 2$. So, $\text{deg } p(x) = \text{deg } q(x) = 2$.
The remainder $r(x) = 0$, and $\text{deg } r(x) = -\infty$, which is less than $\text{deg } g(x) = 0$. The division algorithm is satisfied.
Example:
$p(x) = x^2 + x + 1$
$g(x) = 5$
$q(x) = \frac{1}{5}x^2 + \frac{1}{5}x + \frac{1}{5}$
$r(x) = 0$
(ii) deg q(x) = deg r(x)
Let the degree of $q(x)$ and $r(x)$ be 1. So, $\text{deg } q(x) = 1$ and $\text{deg } r(x) = 1$.
According to the division algorithm, we must have $\text{deg } r(x) < \text{deg } g(x)$. So, we need $\text{deg } g(x) > 1$. Let's choose $\text{deg } g(x) = 2$.
Let $q(x) = x+1$ (degree 1).
Let $r(x) = x$ (degree 1).
Let $g(x) = x^2$ (degree 2). Here $\text{deg } r(x) = 1 < \text{deg } g(x) = 2$.
Now, we find $p(x)$ using the division algorithm: $p(x) = g(x) \times q(x) + r(x)$.
$$p(x) = (x^2) \times (x+1) + x$$
$$p(x) = x^3 + x^2 + x$$
Let's verify the degrees:
$\text{deg } p(x) = 3$
$\text{deg } g(x) = 2$
$\text{deg } q(x) = 1$
$\text{deg } r(x) = 1$
Here, $\text{deg } q(x) = \text{deg } r(x) = 1$, and $\text{deg } r(x) = 1 < \text{deg } g(x) = 2$. The conditions are satisfied.
Example:
$p(x) = x^3 + x^2 + x$
$g(x) = x^2$
$q(x) = x+1$
$r(x) = x$
(iii) deg r(x) = 0
This condition implies that the remainder $r(x)$ is a non-zero constant. Let $r(x) = c$, where $c \neq 0$.
According to the division algorithm, we must have $\text{deg } r(x) < \text{deg } g(x)$. So, we need $0 < \text{deg } g(x)$. This means the degree of $g(x)$ must be at least 1.
Let $\text{deg } r(x) = 0$. Let $r(x) = 7$.
Let $\text{deg } g(x) = 1$. Let $g(x) = x$. Here $\text{deg } r(x) = 0 < \text{deg } g(x) = 1$.
Let's choose a quotient $q(x)$, say $q(x) = x^2$. $\text{deg } q(x) = 2$.
Now, we find $p(x)$ using the division algorithm: $p(x) = g(x) \times q(x) + r(x)$.
$$p(x) = (x) \times (x^2) + 7$$
$$p(x) = x^3 + 7$$
Let's verify the degrees:
$\text{deg } p(x) = 3$
$\text{deg } g(x) = 1$
$\text{deg } q(x) = 2$
$\text{deg } r(x) = 0$
Here, $\text{deg } r(x) = 0$. The remainder condition $\text{deg } r(x) = 0 < \text{deg } g(x) = 1$ is satisfied. The division algorithm $x^3+7 = x(x^2) + 7$ is satisfied.
Example:
$p(x) = x^3 + 7$
$g(x) = x$
$q(x) = x^2$
$r(x) = 7$
Exercise 2.4 (Optional)
Question 1. Verify that the numbers given alongside of the cubic polynomials below are their zeroes. Also verify the relationship between the zeroes and the coefficients in each case:
(i) 2x3 + x2 – 5x + 2; $\frac{1}{2}$ , 1, – 2
(ii) x3 – 4x2 + 5x – 2; 2, 1, 1
Answer:
We will verify if the given numbers are zeroes of the polynomial and then verify the relationship between the zeroes and the coefficients for each case.
(i) $p(x) = 2x^3 + x^2 – 5x + 2$; Zeroes: $\frac{1}{2}$, 1, – 2
The given cubic polynomial is $p(x) = 2x^3 + x^2 – 5x + 2$.
Comparing with the standard form $ax^3 + bx^2 + cx + d$, the coefficients are $a = 2$, $b = 1$, $c = -5$, $d = 2$.
Let the given potential zeroes be $\alpha = \frac{1}{2}$, $\beta = 1$, $\gamma = -2$.
Verification of Zeroes:
Substitute each value into the polynomial $p(x)$. If $p(x_0) = 0$, then $x_0$ is a zero.
For $x = \frac{1}{2}$:
$$p\left(\frac{1}{2}\right) = 2\left(\frac{1}{2}\right)^3 + \left(\frac{1}{2}\right)^2 - 5\left(\frac{1}{2}\right) + 2$$
$$p\left(\frac{1}{2}\right) = 2\left(\frac{1}{8}\right) + \frac{1}{4} - \frac{5}{2} + 2$$
$$p\left(\frac{1}{2}\right) = \frac{1}{4} + \frac{1}{4} - \frac{10}{4} + \frac{8}{4}$$
$$p\left(\frac{1}{2}\right) = \frac{1 + 1 - 10 + 8}{4} = \frac{10 - 10}{4} = \frac{0}{4} = 0$$
So, $\frac{1}{2}$ is a zero.
For $x = 1$:
$$p(1) = 2(1)^3 + (1)^2 - 5(1) + 2$$
$$p(1) = 2(1) + 1 - 5 + 2$$
$$p(1) = 2 + 1 - 5 + 2 = 5 - 5 = 0$$
So, 1 is a zero.
For $x = -2$:
$$p(-2) = 2(-2)^3 + (-2)^2 - 5(-2) + 2$$
$$p(-2) = 2(-8) + 4 + 10 + 2$$
$$p(-2) = -16 + 4 + 10 + 2 = -16 + 16 = 0$$
So, -2 is a zero.
The given numbers $\frac{1}{2}$, 1, and -2 are indeed the zeroes of $p(x)$.
Verification of Relationships between Zeroes and Coefficients:
For a cubic polynomial $ax^3 + bx^2 + cx + d$ with zeroes $\alpha, \beta, \gamma$:
1. Sum of zeroes: $\alpha + \beta + \gamma = -\frac{b}{a}$
2. Sum of the product of zeroes taken two at a time: $\alpha\beta + \beta\gamma + \gamma\alpha = \frac{c}{a}$
3. Product of zeroes: $\alpha\beta\gamma = -\frac{d}{a}$
Using the zeroes $\alpha = \frac{1}{2}, \beta = 1, \gamma = -2$ and coefficients $a = 2, b = 1, c = -5, d = 2$:
Sum of zeroes: $\alpha + \beta + \gamma = \frac{1}{2} + 1 + (-2) = \frac{1}{2} - 1 = -\frac{1}{2}$.
From coefficients: $-\frac{b}{a} = -\frac{1}{2}$.
$$\alpha + \beta + \gamma = -\frac{b}{a}$$
... (Verified)
Sum of the product of zeroes taken two at a time:
$$\alpha\beta + \beta\gamma + \gamma\alpha = \left(\frac{1}{2}\right)(1) + (1)(-2) + (-2)\left(\frac{1}{2}\right)$$
$$= \frac{1}{2} - 2 - 1 = \frac{1}{2} - 3 = \frac{1 - 6}{2} = -\frac{5}{2}$$
From coefficients: $\frac{c}{a} = \frac{-5}{2}$.
$$\alpha\beta + \beta\gamma + \gamma\alpha = \frac{c}{a}$$
... (Verified)
Product of zeroes:
$$\alpha\beta\gamma = \left(\frac{1}{2}\right)(1)(-2) = -1$$
From coefficients: $-\frac{d}{a} = -\frac{2}{2} = -1$.
$$\alpha\beta\gamma = -\frac{d}{a}$$
... (Verified)
(ii) $p(x) = x^3 – 4x^2 + 5x – 2$; Zeroes: 2, 1, 1
The given cubic polynomial is $p(x) = x^3 – 4x^2 + 5x – 2$.
Comparing with the standard form $ax^3 + bx^2 + cx + d$, the coefficients are $a = 1$, $b = -4$, $c = 5$, $d = -2$.
Let the given potential zeroes be $\alpha = 2$, $\beta = 1$, $\gamma = 1$.
Verification of Zeroes:
Substitute each distinct value into the polynomial $p(x)$.
For $x = 2$:
$$p(2) = (2)^3 - 4(2)^2 + 5(2) - 2$$
$$p(2) = 8 - 4(4) + 10 - 2$$
$$p(2) = 8 - 16 + 10 - 2 = 18 - 18 = 0$$
So, 2 is a zero.
For $x = 1$:
$$p(1) = (1)^3 - 4(1)^2 + 5(1) - 2$$
$$p(1) = 1 - 4(1) + 5 - 2$$
$$p(1) = 1 - 4 + 5 - 2 = 6 - 6 = 0$$
So, 1 is a zero. Since it appears twice in the list, it is a zero with multiplicity 2.
The given numbers 2, 1, and 1 are indeed the zeroes of $p(x)$.
Verification of Relationships between Zeroes and Coefficients:
Using the zeroes $\alpha = 2, \beta = 1, \gamma = 1$ and coefficients $a = 1, b = -4, c = 5, d = -2$:
Sum of zeroes: $\alpha + \beta + \gamma = 2 + 1 + 1 = 4$.
From coefficients: $-\frac{b}{a} = -\frac{(-4)}{1} = 4$.
$$\alpha + \beta + \gamma = -\frac{b}{a}$$
... (Verified)
Sum of the product of zeroes taken two at a time:
$$\alpha\beta + \beta\gamma + \gamma\alpha = (2)(1) + (1)(1) + (1)(2)$$
$$= 2 + 1 + 2 = 5$$
From coefficients: $\frac{c}{a} = \frac{5}{1} = 5$.
$$\alpha\beta + \beta\gamma + \gamma\alpha = \frac{c}{a}$$
... (Verified)
Product of zeroes:
$$\alpha\beta\gamma = (2)(1)(1) = 2$$
From coefficients: $-\frac{d}{a} = -\frac{(-2)}{1} = 2$.
$$\alpha\beta\gamma = -\frac{d}{a}$$
... (Verified)
Question 2. Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time, and the product of its zeroes as 2, –7, –14 respectively.
Answer:
Let the cubic polynomial be $p(x) = ax^3 + bx^2 + cx + d$, where $a \neq 0$. Let its zeroes be $\alpha$, $\beta$, and $\gamma$.
The relationships between the zeroes and coefficients of a cubic polynomial are:
Sum of zeroes: $\alpha + \beta + \gamma = -\frac{b}{a}$
Sum of the product of zeroes taken two at a time: $\alpha\beta + \beta\gamma + \gamma\alpha = \frac{c}{a}$
Product of zeroes: $\alpha\beta\gamma = -\frac{d}{a}$
We are given the following values:
Sum of zeroes ($\alpha + \beta + \gamma$) = 2
Sum of the product of zeroes taken two at a time ($\alpha\beta + \beta\gamma + \gamma\alpha$) = -7
Product of zeroes ($\alpha\beta\gamma$) = -14
A cubic polynomial can be constructed using the formula:
$$p(x) = k[x^3 - (\text{Sum of zeroes})x^2 + (\text{Sum of product of zeroes taken two at a time})x - (\text{Product of zeroes})]$$
$$p(x) = k[x^3 - (\alpha + \beta + \gamma)x^2 + (\alpha\beta + \beta\gamma + \gamma\alpha)x - \alpha\beta\gamma]$$
where $k$ is any non-zero real number.
Substitute the given values into the formula:
$$p(x) = k[x^3 - (2)x^2 + (-7)x - (-14)]$$
$$p(x) = k[x^3 - 2x^2 - 7x + 14]$$
Since the question asks for 'a' cubic polynomial, we can choose the simplest non-zero value for $k$, which is $k=1$.
Setting $k=1$, the polynomial is:
$$p(x) = 1 \times (x^3 - 2x^2 - 7x + 14)$$
$$p(x) = x^3 - 2x^2 - 7x + 14$$
Final Answer: A cubic polynomial satisfying the given conditions is $x^3 - 2x^2 - 7x + 14$.
Question 3. If the zeroes of the polynomial x3 – 3x2 + x + 1 are a – b, a, a + b, find a and b.
Answer:
Given:
The cubic polynomial is $p(x) = x^3 – 3x^2 + x + 1$.
The zeroes of the polynomial are $a-b$, $a$, and $a+b$.
To Find: The values of $a$ and $b$.
Solution:
The given polynomial is $p(x) = x^3 – 3x^2 + x + 1$.
Comparing this with the standard form of a cubic polynomial $Ax^3 + Bx^2 + Cx + D$, we identify the coefficients:
$A = 1$
$B = -3$
$C = 1$
$D = 1$
Let the zeroes of the polynomial be $\alpha = a-b$, $\beta = a$, and $\gamma = a+b$.
We use the relationships between the zeroes and the coefficients of a cubic polynomial:
1. Sum of zeroes: $\alpha + \beta + \gamma = -\frac{B}{A}$
2. Product of zeroes: $\alpha\beta\gamma = -\frac{D}{A}$
Using the sum of zeroes relationship:
$$(a-b) + (a) + (a+b) = -\frac{-3}{1}$$
$$a - b + a + a + b = 3$$
$$3a = 3$$
Dividing by 3:
$a = 1$
... (i)
Now that we have the value of $a$, the zeroes are $1-b$, $1$, and $1+b$.
Using the product of zeroes relationship:
$$(a-b)(a)(a+b) = -\frac{D}{A}$$
Substitute the value of $a$ from (i) and the values of $D$ and $A$:
$$(1-b)(1)(1+b) = -\frac{1}{1}$$
$$(1-b)(1+b) = -1$$
Using the algebraic identity $(x-y)(x+y) = x^2 - y^2$ on the left side:
$$1^2 - b^2 = -1$$
$$1 - b^2 = -1$$
Rearrange the equation to solve for $b^2$:
$$1 + 1 = b^2$$
$$2 = b^2$$
Taking the square root of both sides:
$b = \pm \sqrt{2}$
... (ii)
The value of $a$ is 1. The value of $b$ can be either $\sqrt{2}$ or $-\sqrt{2}$. Both values result in the same set of zeroes $\{1-\sqrt{2}, 1, 1+\sqrt{2}\}$.
Final Answer: $a = 1$ and $b = \pm \sqrt{2}$.
Question 4. If two zeroes of the polynomial x4 – 6x3 – 26x2 + 138x – 35 are 2 ± $\sqrt{3}$ , find other zeroes.
Answer:
Given:
The polynomial is $p(x) = x^4 – 6x^3 – 26x^2 + 138x – 35$.
Two of the zeroes are $2 + \sqrt{3}$ and $2 - \sqrt{3}$.
To Find: The other zeroes of the polynomial.
Solution:
Since $2 + \sqrt{3}$ and $2 - \sqrt{3}$ are zeroes of the polynomial $p(x)$, then by the Factor Theorem, $(x - (2 + \sqrt{3}))$ and $(x - (2 - \sqrt{3}))$ are factors of $p(x)$.
The product of these factors is also a factor of $p(x)$. Let's find the product:
$$G(x) = [x - (2 + \sqrt{3})][x - (2 - \sqrt{3})]$$
$$G(x) = [(x - 2) - \sqrt{3}][(x - 2) + \sqrt{3}]$$
Using the algebraic identity $(a - b)(a + b) = a^2 - b^2$, where $a = (x - 2)$ and $b = \sqrt{3}$:
$$G(x) = (x - 2)^2 - (\sqrt{3})^2$$
Expand $(x - 2)^2$ and calculate $(\sqrt{3})^2$:
$$G(x) = (x^2 - 4x + 4) - 3$$
$$G(x) = x^2 - 4x + 1$$
So, $x^2 - 4x + 1$ is a factor of $p(x)$.
To find the other zeroes, we divide the polynomial $p(x)$ by the factor $x^2 - 4x + 1$ using polynomial long division. The quotient will give us a polynomial whose zeroes are the remaining zeroes of $p(x)$.
Divide $x^4 – 6x^3 – 26x^2 + 138x – 35$ by $x^2 - 4x + 1$:
$$ \begin{array}{r} x^2 - 2x - 35\phantom{)} \\ x^2-4x+1{\overline{\smash{\big)}\,x^4-6x^3-26x^2+138x-35\phantom{)}}} \\ \underline{-~\phantom{()}(x^4-4x^3+x^2)\phantom{-b)}} \\ -2x^3-27x^2+138x-35\phantom{)} \\ \underline{-~\phantom{()}(-2x^3+8x^2-2x)} \\ -35x^2+140x-35\phantom{)} \\ \underline{-~\phantom{()}(-35x^2+140x-35)} \\ 0\phantom{)} \end{array} $$The remainder is 0, which confirms that $x^2 - 4x + 1$ is a factor of $p(x)$.
The quotient is $q(x) = x^2 - 2x - 35$.
The remaining zeroes of $p(x)$ are the zeroes of the quotient polynomial $q(x) = x^2 - 2x - 35$.
To find the zeroes of $q(x)$, we set $q(x) = 0$:
$$x^2 - 2x - 35 = 0$$
We can factor this quadratic equation. We look for two numbers whose product is $-35$ and whose sum is $-2$. These numbers are $-7$ and $5$.
Rewrite the middle term $-2x$ as $-7x + 5x$:
$$x^2 - 7x + 5x - 35 = 0$$
Group the terms and factor:
$$x(x - 7) + 5(x - 7) = 0$$
Factor out the common binomial factor $(x - 7)$:
$$(x - 7)(x + 5) = 0$$
Set each factor equal to zero to find the zeroes:
Case 1: $x - 7 = 0$
$$x = 7$$
Case 2: $x + 5 = 0$
$$x = -5$$
The other two zeroes of the polynomial $p(x)$ are 7 and -5.
Final Answer: The other zeroes of the polynomial are 7 and -5.
Question 5. If the polynomial x4 – 6x3 + 16x2 – 25x + 10 is divided by another polynomial x2 – 2x + k, the remainder comes out to be x + a, find k and a.
Answer:
Given:
Dividend $p(x) = x^4 – 6x^3 + 16x^2 – 25x + 10$
Divisor $g(x) = x^2 – 2x + k$
Remainder $r(x) = x + a$
To Find: The values of $k$ and $a$.
Solution:
According to the Division Algorithm for Polynomials, we have the relationship:
$$p(x) = g(x) \times q(x) + r(x)$$$
... (i)
where $q(x)$ is the quotient and $r(x)$ is the remainder.
Rearranging equation (i), we get:
$$p(x) - r(x) = g(x) \times q(x)$$$
This implies that $p(x) - r(x)$ is exactly divisible by $g(x)$, and the remainder of this division should be 0.
First, let's calculate $p(x) - r(x)$:
$$p(x) - r(x) = (x^4 – 6x^3 + 16x^2 – 25x + 10) - (x + a)$$$
$$p(x) - r(x) = x^4 – 6x^3 + 16x^2 – 25x + 10 - x - a$$
Combine like terms:
$$p(x) - r(x) = x^4 – 6x^3 + 16x^2 + (-25x - x) + (10 - a)$$$
$$p(x) - r(x) = x^4 – 6x^3 + 16x^2 – 26x + (10 - a)$$$
Now, we perform polynomial long division of $p(x) - r(x) = x^4 – 6x^3 + 16x^2 – 26x + (10 - a)$ by $g(x) = x^2 – 2x + k$. The remainder of this division must be 0.
$$ \begin{array}{r} x^2 - 4x + (8-k)\phantom{)} \\ x^2-2x+k{\overline{\smash{\big)}\,x^4-6x^3+16x^2-26x+(10-a)\phantom{)}}} \\ \underline{-~\phantom{()}(x^4-2x^3+kx^2)\phantom{-b)}} \\ -4x^3+(16-k)x^2-26x+(10-a)\phantom{)} \\ \underline{-~\phantom{()}(-4x^3+8x^2-4kx)} \\ (16-k-8)x^2+(-26+4k)x+(10-a)\phantom{)} \\ (8-k)x^2+(4k-26)x+(10-a)\phantom{)} \\ \underline{-~\phantom{()}((8-k)x^2-2(8-k)x+k(8-k))} \\ (4k-26 - (16-2k))x + (10-a - (8k-k^2))\phantom{)} \\ (4k-26-16+2k)x + (10-a-8k+k^2)\phantom{)} \\ (6k-42)x + (k^2-8k-a+10)\phantom{)} \end{array} $$Wait, let me redo the subtraction in the long division carefully, specifically the third step.
$$ \begin{array}{r} x^2 - 4x + (8-k)\phantom{)} \\ x^2-2x+k{\overline{\smash{\big)}\,x^4-6x^3+16x^2-26x+(10-a)\phantom{)}}} \\ \underline{-~\phantom{()}(x^4-2x^3+kx^2)\phantom{-b)}} \\ -4x^3+(16-k)x^2-26x+(10-a)\phantom{)} \\ \underline{-~\phantom{()}(-4x^3+8x^2-4kx)} \\ (16-k-8)x^2+(-26+4k)x+(10-a)\phantom{)} \\ (8-k)x^2+(4k-26)x+(10-a)\phantom{)} \\ \underline{-~\phantom{()}((8-k)x^2-2(8-k)x+k(8-k))} \\ (8-k)x^2+(4k-26)x+(10-a) - (8-k)x^2 + 2(8-k)x - k(8-k)\phantom{)} \\ (4k-26 + 16-2k)x + (10-a - (8k-k^2))\phantom{)} \\ (2k-10)x + (k^2-8k-a+10)\phantom{)} \end{array} $$The remainder obtained from the long division is $(2k - 10)x + (k^2 - 8k - a + 10)$.
Since $p(x) - r(x)$ is divisible by $g(x)$, this remainder must be equal to the zero polynomial (0).
For a polynomial to be zero, all its coefficients must be zero.
Equating the coefficient of $x$ to zero:
$$2k - 10 = 0$$
... (ii)
From equation (ii):
$$2k = 10$$
$$k = \frac{10}{2}$$$
$$k = 5$$
... (iii)
Equating the constant term to zero:
$$k^2 - 8k - a + 10 = 0$$
... (iv)
Substitute the value of $k$ from equation (iii) into equation (iv):
$$(5)^2 - 8(5) - a + 10 = 0$$
$$25 - 40 - a + 10 = 0$$
$$-15 - a + 10 = 0$$
$$-5 - a = 0$$
$$-a = 5$$
$$a = -5$$
... (v)
The values of $k$ and $a$ are 5 and -5 respectively.
Final Answer: $k = 5$ and $a = -5$.

